2580.51 – A Hard Functional Equation

The function ff satisfies the functional equation

f(x)+ f(y)= f(x + y)− xy −1f(x) + f(y) = f(x + y) - xy - 1

for every pair x, yx, y of real numbers. If in addition f(1)=1f(1) = 1, then the number of positive integers nn for which f(n)= nf(n) = n is:

  1. 0

  2. 1

  3. 2

  4. 3

  5. infinite

Solution

We are given f(1)=1f(1) = 1. Let's find some more of this function's values.

f(x)+f(y)= f(x+y)− xy −1f(x)+f(0)= f(x+0)− x⋅0−1= f(x)−1\begin{aligned} f(x) + f(y) &= f(x + y) - xy - 1 \\f(x) + f(0) &= f(x + 0) - x \cdot 0 - 1 \\&= f(x) - 1\end{aligned}

So f(0)=−1f(0) = -1.

f(1)+f(1)= f(2)−1⋅1−11+1= f(2)−1−1\begin{aligned}f(1) + f(1) &= f(2) - 1 \cdot 1 - 1 \\1 + 1 &= f(2) - 1 - 1\end{aligned}

So f(2)=4.f(2) = 4.

f(2)+ f(1)= f(3)−2⋅1−14+1= f(3)−2−1\begin{aligned}f(2) + f(1) &= f(3) - 2 \cdot 1 - 1\\4 + 1 &= f(3) - 2 - 1\end{aligned}

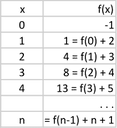
So f(3)=8f(3) = 8. We've made a chart (see below) in order to look for a pattern. We see that for f(n)= nf(n) = n, we have to have:

f(n)= f(n−1)+ n +1= n,f(n) = f(n - 1) + n + 1 = n,

so f(n−1)+1=0f(n - 1) + 1 = 0, and f(n−1)=−1f(n - 1) = -1. We see that n =1n = 1 works and no other positive integers will work.

The answer is (b).