3450.21 – Tetrahedron Inscribed in a Cube

Four of the eight vertexes of a cube are the vertexes of a regular tetrahedron as in the figure below. Relax for a moment and enjoy how neatly the regular tetrahedron fits inside the cube. The other four vertexes of the cube, incidentally, form a second, inter-penetrating tetrahedron.

Find the ratio of the surface area of the cube to the surface area of the tetrahedron.

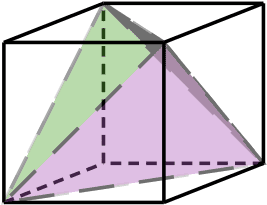
Solution

Let the edge of the cube be $x$ . Then $SC$ , the surface area of the cube, is $6x^2$ .

The faces of the tetrahedron are equilateral triangles whose edges are diagonals of the cube's square faces. If $y$ is the edge length of the tetrahedron, then $y = x\sqrt{2}$ since the diagonal of a square's face is the hypotenuse of a 45-45-90 triangle. Now the area of an equilateral triangle of edge $y$ is $y^2 \sqrt{3}/4 = x^2 \sqrt{3}/2$ so $ST$ , the surface area of the tetrahedron, is $ST = 4 x^2 \sqrt{3}/2 = 2 x^2 \sqrt{3}.$

Thus the desired ratio of areas is

$\frac{SC}{ST} = \frac{6x^2}{2 x^2 \sqrt{3}} = \frac{3}{\sqrt{3}} = \sqrt{3}.$

Students who like making models might make a nice 3-d model of this figure.

(N.b. the 45-45-90 right triangle is sometimes known as the western, or cowboy's, triangle. Why?)