3590.11 – Parallelogram and a Geometric Mean

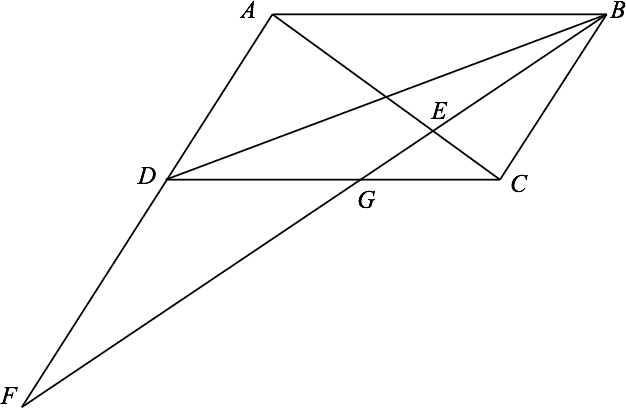
Given parallelogram ABCD with its diagonals drawn. A line through B intersects AC at E, DC at G, and line AD extended at F. Observe that triangle AEF is similar to triangle CEB and show that EB is the geometric mean of EG and EF. Interested? See how this looks in a drawing.

Solution

We want $EB = \sqrt{EG \cdot EF}$ , i.e. $EB^2 = EG \cdot EF$ , i.e. $\frac{EF}{EB} = \frac {EB}{EG}$ .

We tease out some similar triangles to make this happen. There are many congruent angles to work with. Find them and use them!

First, $\triangle AEF \sim \triangle CEB$ , so $\frac{EF}{EB} = \frac{EA}{CE}$ .

Then, $\triangle CEG \sim \triangle AEB$ , so $\frac{EA}{CE} = \frac{EB}{EG}$ .

So $\frac{EF}{EB} = \frac{EB}{EG}$ , and there we are.

Hmm, what if $F = D$ ?