3650.23 – Big Rectangular Solid

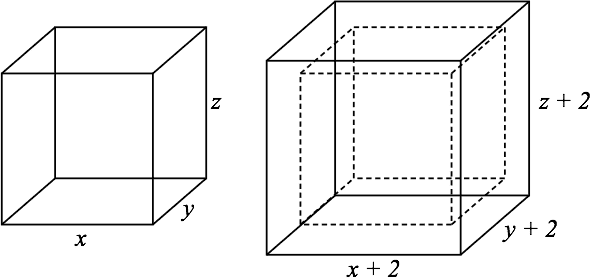
Imagine a rectangular solid composed of small unit cubes. The rectangle measures $x$ cubes by $y$ cubes by $z$ cubes. Now imagine building a shell of unit cubes around the entire solid. In other words, the shell is 1 cube thick in all dimensions.

First: what is an equation for the number of unit cubes in the shell in terms of $x$ , $y$ , and $z$ ? Second: for what $x$ , $y$ , and $z$ is the number of cubes in the rectangular solid equal to the number of cubes in the shell?

Solution

The original solid has $xyz$ unit cubes. The new one (see the figure), cube plus shell, has

$(x+2)(y+2)(z+2) = (xy + 2x + 2y + 4)(z + 2) = xyz + 2xy + 2xz + 4x + 2yz + 4y + 4z + 8.$

unit cubes. So the shell alone has $2(xy + xz + yz) + 4(x + y + z) + 8$ cubes. That answers the first question.

As for the second: when does the shell alone equals the original cube in volume, this requires that we solve the equation:

$xyz = 2(xy + xz + yz) + 4(x + y + z) + 8,$

in three variables, which is, $um$ , not easily solved and we're not going to try.

It would be an interesting exercise to program a spreadsheet and fool around with different dimensions to see if anything turns up. Also, try having the original solid be a cube itself, i.e. $x = y = z$ . Then

$x^3 = 6x^2 + 12x + 8$ . $Hmmm$ . Programming a spreadsheet gives us x between 7 and 8, with no integer solution. But there is an explicit solution. Mathematica gives

$x = 2(1 + \sqrt[3]{2} + \sqrt[3]{4}).$