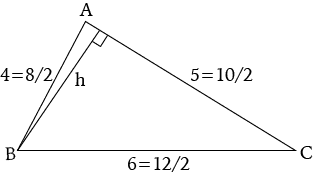
It so happens that the triangle whose sides are 4, 5, and 6 has a special property: its largest angle is twice its smallest angle. Make calculations that support this assertion.
Solution
Let be the largest angle; the smallest.
First Solution. We can use the law of cosines—twice.
\begin{aligned}
6^2 &=& 4^2 + 5^2 - 2 \cdot 4 \cdot 5 \cos A, \
\cos A &=& \frac{6^2 - 4^2 - 5^2}{-2 \cdot 4 \cdot 5} = 0.125, \
\angle A &=& \arccos(0.125) \approx 82.82°. \
&& \
4^2 &=& 5^2 + 6^2 - 2 \cdot 5 \cdot 6 \cos C, \
\cos C &=& \frac{4^2 - 5^2 - 6^2}{-2 \cdot 5 \cdot 6} = 0.75, \
\angle C &=& \arccos(0.75) \approx 41.41°.
\end{aligned}
Voila!
Second Solution. First we find the area, , via Heron's formula. Let be the semi-perimeter of the triangle, i.e., . Then,
\begin{aligned}
\mathcal{A} &=& \sqrt{s (s - a)(s - b)(s - c)}, \
&=& \sqrt{\frac{15}{2} \cdot \frac{3}{2} \cdot \frac{5}{2} \cdot \frac{7}{2}} = \frac{15 \sqrt{7}}{4}.
\end{aligned}
Now we can find the height, , as in figure below. Since
it follows that Now,
\begin{aligned}
\sin A &=& h/4 = 3 \sqrt 7 / 8, \
\angle A &\approx& 82.82° . \
&& \
\sin C &=& h/6 = 3 \sqrt 7 / 12, \
\angle C &\approx& 41.41°.
\end{aligned}
Hey! These solutions are a good advertisement for the law of cosines, don't you agree?